Hydraulic calculation of the pipeline. Pipe hydraulic resistance

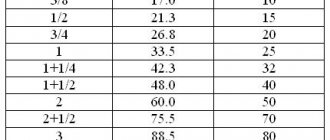
Types of heating systems

Engineering calculation tasks of this kind are complicated by the high diversity of heating systems, both in terms of scale and configuration. There are several types of heating junctions, each of which has its own laws:

1. A two-pipe dead-end system is the most common version of the device, well suited for organizing both central and individual heating circuits.

Two-pipe dead-end heating system

2. The single-pipe system or “Leningradka” is considered the best way to install civil heating systems with a thermal power of up to 30–35 kW.

Single-pipe heating system with forced circulation: 1 - heating boiler; 2 - security group; 3 - heating radiators; 4 — Mayevsky crane; 5 - expansion tank; 6 - circulation pump; 7 - drain

3. A two-pipe system of the associated type is the most material-intensive type of decoupling of heating circuits, which is distinguished by the highest known stability of operation and quality of coolant distribution.

Two-pipe associated heating system (Tichelman loop)

4. Beam distribution is in many ways similar to a two-pipe train, but at the same time, all system controls are located at one point - at the collector unit.

Radial heating circuit: 1 - boiler; 2 - expansion tank; 3 - supply manifold; 4 — heating radiators; 5 — return manifold; 6 - circulation pump

Before we get into the application side of the calculations, we need to make a couple of important warnings. First of all, you need to understand that the key to high-quality calculations lies in understanding the principles of operation of liquid systems on an intuitive level. Without this, consideration of each individual outcome turns into an interweaving of complex mathematical calculations. Secondly, it is practically impossible to present more than basic concepts within one review; for more detailed explanations, it is better to refer to the following literature on the calculation of heating systems:

Pyrkov V.V. “Hydraulic control of heating and cooling systems. Theory and practice" 2nd edition, 2010
R. Yaushovets “Hydraulics is the heart of water heating.”
Manual “Hydraulics of Boiler Houses” from De Dietrich.
A. Savelyev “House heating. Calculation and installation of systems.”

Coefficient of hydraulic friction.

To determine the hydraulic resistance from friction against the pipe walls S tr, it is necessary to know the Darcy parameter λ - the coefficient of hydraulic friction along the length.

The technical literature contains a significant number of formulas from different authors, which are used to calculate the coefficient of hydraulic friction in various ranges of Reynolds numbers.

Designations in the table:

Re – Reynolds number;
k – equivalent roughness of the inner pipe wall (average height of the projections), m.

Another interesting formula for calculating the coefficient of hydraulic friction is given in [1]:

λ=0.11·[(68/Re+ k / D +(1904/ Re )14)/(115·(1904/ Re )10+1)]0.25

Vyacheslav Leonidovich performed verification calculations and found that the above formula is the most universal in a wide range of Reynolds numbers!

The values obtained using this formula are extremely close to the values:

functions λ=64/Re for the zone of laminar flow in the range 10< Re <1500;
functions λ=0.11·(68/Re+ k / D )0.25 for the zone of turbulent flow at Re >4500;
in the range 1500< Re <4500, according to the analysis, there is a transition zone.

In the transition zone, according to Nikuradze’s experiments, the graph of the function λ= f (Re,D, k ) has a complex shape. It represents two conjugate reverse curves, which in turn are conjugated on one side with the curve of smooth pipes (laminar flow), and on the other side with straight lines of relative roughness.

This zone has not been fully studied, so it is advisable to calculate the hydraulic modes of the designed systems without entering this area: 1500< Re <4500!

The following figure shows graphs of the function λ= f (Re,D, k ) constructed using the above universal formula. The nature of the curves in the transition region corresponds to the Nikuradze graphs [2, 4].

The custom function in Excel KtrPipeWater(Rvoda,twater,G,D,ke) calculates the coefficient of hydraulic friction λ using the considered universal formula. In this case, everywhere further k e = k .

Attention!

λ changes , which can cause inoperability of automatic control systems!
PF KtrPipeWater(Pwater,twater,G,D,ke) with turbulent flow significantly depends on the value of ke - the equivalent roughness of the inner surface of the pipe. In this regard, you should pay attention to setting the objective value of ke , taking into account the pipes used during installation (see [2] pp. 78÷83).

Calculation of hydraulic resistance in Excel.

To facilitate routine hydraulic calculations, V.L. Polkovov. developed a number of user functions. A list of some of them, most often used in practice, is given in the table below.

Some clarifications on custom function arguments:

GS diffuser (Pwater,twater,G,Dmin,Dmax,ke,L) – free dimensions;
GStransitionDiffuser(Pwater,twater,G,Dmin,Dmax,ke) – standard transition;
GSconfuser(Pwater,twater,G,Dmin,Dmax,ke,L) – free dimensions;
GStransitionConfusor(Pwater,twater,G,Dmin,Dmax,ke) – standard transition;
GSoutlet(Pwater,twater,G,D0,R0,Angle,ke) – free dimensions;
GSotvodGOST(Pwater,twater,G,D,Angle,ke) – standard outlet.

It is advisable to use the given user functions taking into account the initial transportation section (the distance from one hydraulic resistance to the next hydraulic resistance). This makes it possible to reduce calculation errors caused by the influence of the “unsteady” nature of the fluid flow.

For turbulent flows, the length of the initial section must be at least:

Lstart=(7.88 lg (Re) – 4.35) D

For laminar flows, the minimum length of the initial section:

Lstart=B·Re·D

Here B = 0.029 according to Boussinex, and B = 0.065 according to Schiller, D is the internal diameter of the transportation system.

The following screenshot shows an Excel table with examples of hydraulic resistance calculations.

Literature:

Chernikin A.V. Generalization of the calculation of the hydraulic resistance coefficient of pipelines // Science and technology of hydrocarbons. M.: 1998. No. 1. pp. 21–23.
I.E. Idelchik, “Handbook of hydraulic resistance.” 3rd edition, revised and expanded. Moscow, Mechanical Engineering, 1992.
HELL. Altshul, “Hydraulic Resistance”, second edition, revised and expanded. Moscow, NEDRA, 1982.
B.N. Lobaev, Doctor of Technical Sciences, Professor, “Calculation of pipelines for water and steam heating systems.” State publishing house of literature on construction and architecture. Ukrainian SSR, Kyiv, 1956.

Link to download the file: gidravlicheskie-soprotivleniya (xls 502.0KB).

Articles with similar topics

Calculation of a pipeline with parallel sections
Hydraulic calculation of pipelines