What is Gcal
The cost of heating is important for residents of high-rise buildings with central coolant supply
The concept gigacalorie means a unit of measurement of thermal energy in heating. This energy within the room is transferred by convection from batteries to objects and radiated into the air. A calorie is the amount of energy required to warm 1 g of water by 1 degree at atmospheric pressure.
To calculate thermal energy, another unit is used - Gcal, equal to 1 billion calories. On average, heat consumption per 1 sq. m in Gcal in the Russian Federation is 0.9342 Gcal/month. If we convert the indicator into other values, 1 Gcal will be equal to:
- 1162.2 kW/h;
- heating 1 thousand tons of water to +1 degree.
The value was approved in 1995.
Features of Gcal for residential high-rise buildings
The thermostat allows you to control the flow of coolant and temperature.
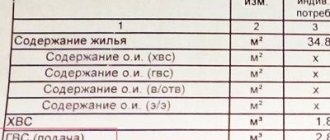
If a multi-apartment building is not equipped with a common building or individual meter, thermal energy is calculated based on the area of the premises. When there is a metering device, horizontal or sequential route routing, residents independently determine the amount of thermal energy. For this we use:
- Throttling of radiators. When traffic is limited, the temperature decreases and energy consumption decreases.
- A general thermostat is installed on the return line. Coolant consumption depends on the temperature in the apartment. At low flow rates the temperature is higher, at high flow rates it is lower.
An apartment in a new building is mainly equipped with an individual meter.
Specifics of Gcal for a private home
The cheapest fuel in terms of gigacalories are pellets.
The material spent on heating is determined by the tariff for private buildings. According to average data, the cost of 1 Gcal is equal to:
- gas – natural 3.3 thousand rubles, liquefied 520 rubles;
- solid fuel - coal 550 rubles, pellets 1.8 thousand rubles;
- diesel – 3270 rub.;
- electricity – 4.3 thousand rubles.
The price of thermal energy depends on the region in which a private house is located.
Conserving energy: the first law of thermodynamics
The first law of thermodynamics is, simply put, the law of conservation of energy. He claims that energy does not disappear anywhere. When thermal energy ( Q ) is absorbed or released by the system, and the system itself performs work ( W ) on the surrounding bodies (or, conversely, the surrounding bodies perform work on it), then the internal energy of the system, which had the initial value ( U_н ), becomes equal to (U_к) as follows:
Chapter 8 talks a lot about the conservation of mechanical energy. It shows that the total mechanical energy (the sum of potential and kinetic energy) is conserved. To claim this, it was necessary to work with systems where energy is not wasted on heating - for example, when there is no friction. Now everything has changed. Thermal energy is finally taken into account (as you probably realized from the discussion), and now the total energy of the system can be considered taking into account the transfer of thermal energy, the work done and the internal energy of the system.
Based on the combination of these three quantities (thermal energy, work and internal energy), the total energy of the system is determined, which is generally conserved. If you transfer to the system an amount of thermal energy equal to (Q), then in the absence of work its amount of internal energy, denoted as (U), will change to (Q). The system can lose energy by performing work on surrounding bodies, for example when a machine lifts a load hanging at the end of a rope. So, when the system performs work on the surrounding bodies and does not waste any thermal energy, its internal energy (U) will change to (W). In other words, if we take into account thermal energy, then taking into account all these three quantities (thermal energy, work and internal energy), the total energy of the system is conserved.
The usefulness of the first law of thermodynamics is that it relates all three basic quantities: thermal energy, work and internal energy. Knowing two of them, you can always determine the third.
The amount of thermal energy transferred (Q) is positive or negative when the system absorbs or releases thermal energy, respectively. The amount of work (W) is positive or negative when work, respectively, is done by the system on surrounding bodies or by surrounding bodies on the system.
Beginners often get confused when trying to determine whether each quantity is positive or negative. To avoid confusion, when working with the first law of thermodynamics, it is recommended to proceed from the general idea of conservation of energy. Let us assume that the motor performs 2000 J of work on the surrounding bodies, releasing 3000 J of thermal energy. How much does its internal energy change? In this case, it is known that the motor performs 2000 J of work on the surrounding bodies, so it is clear that its internal energy decreases by 2000 J. In addition, while performing work, it also releases 3000 J of thermal energy, so the internal energy of the motor decreases by another 3000 J.
The values of work and transferred thermal energy should be considered negative. Then in the previous example we obtain the following change in internal energy:
The internal energy of the system decreases by 5000 J, which definitely makes sense, since the system performs 2000 J of work on the surrounding bodies and releases 3000 J of thermal energy. On the other hand, what if the system, performing 2000 J of work on the surrounding bodies, absorbs 3000 J of their thermal energy? In this case, there would be 2000 J of incoming and 3000 J of outgoing energy. Now it’s clear what the signs should be:
In this case, the total change in the internal energy of the system is +1000 J. Work takes on a negative value when it is performed on the system by surrounding bodies. For example, the system absorbs 3000 J, while the surrounding bodies do 4000 J of work on it. This means that the internal energy of the system increases by 3000 J + 4000 J = 7000 J. And if you need to calculate everything, then use the following formula:
and then note that since the surrounding bodies are doing work on the system, the value of ( W ) is considered negative. Thus we get:
This chapter deals with processes in which analysis requires working with parameters such as volume, pressure, temperature and energy. Moreover, the results obtained very much depend on how these values change. For example, if a gas does work while keeping its volume constant, then this process will differ from one in which not the volume, but the pressure of the gas remains constant.
In thermodynamics, four standard regimes are usually considered, which differ in the constancy of one of the above parameters (pressure, volume, temperature and energy).
Please note that the changes in the processes described in the following sections are called quasi-static, i.e. these changes occur quite slowly, allowing the pressure and temperature to remain the same anywhere in the system.
A process in which the pressure remains constant is called isobaric (“baric” means “relating to pressure”). In Fig. Figure 15.1 shows a cylinder with a piston that is lifted by some gas when the gas is heated. The volume of gas changes, but the weighted piston keeps the pressure constant.
What work does the system do when the gas expands? Work is equal to the product of ( F ) by ( s ), meaning force and displacement, respectively. In addition, force is equal to ( P ) times ( A ), meaning pressure and area, respectively. It means that:
But the product of area ( A ) and displacement ( s ) is equal to the change in volume ( Delta!V ). Thus:
An isobaric process can be shown as a graph (as in Fig. 15.2), which shows that the volume changes while the pressure remains constant. Since ( W=PDelta!V ), the work is the area limited by the schedule.
Let's say there are 60 m3 of ideal gas under a pressure of 200 Pa (see Chapter 2), which is heated until it expands to a volume of 120 m3 (( PV= nRT ), where ( n ), ( R ) and ( T ) stand for the number of moles, the universal gas constant (8.31), and temperature, respectively; see Chapter 14). What work does the gas do? All you need to do is plug in the numbers into the formula:
Expanding at constant pressure, the gas does 12,000 J of work.
What if the pressure in the system is not constant? After all, it is not very common to come across devices with a weighted piston, as in Fig. 15.1. Most often you have to deal with a simple closed vessel, as in Fig. 15.3, which shows a can of deodorant that someone carelessly threw into a fire. In this case, the volume remains constant, and such a process is called isochoric. As the gas inside the canister heats up, its pressure increases, but the volume remains constant (unless, of course, the canister explodes).
What work is done with a spray can? Look at the graph (Figure 15.4). In this case, the volume is constant, so ( Fs ) (the product of force and displacement) is zero. No work is done—the area under the graph is zero.
In an isothermal process, the temperature remains constant while other quantities change. Look at the wonderful apparatus shown in Fig. 15.5. This device is specially designed to keep the gas temperature constant, even when the piston rises. As thermal energy is added to (or removed from the system) the piston is slowly raised (or slowly lowered) so that the product of pressure and volume remains constant. Since (PV= nRT) (see Chapter 14), the temperature also remains constant.
What work is done when volume changes? Since (PV= nRT), we get the following relationship between ( P ) and ( V ):
This formula is illustrated by the graph shown in Fig. 15.6.
The work performed is “showed” by the area under the graph. But what is the area of this area? The work performed is determined by the following formula, where ( ln ) is the natural logarithm, ( R ) is the gas constant (8.31), ( V_1 ) and ( V_0 ) mean the final and initial volume, respectively:
Since in an isothermal process the temperature remains constant and the internal energy of an ideal gas is ( (3/2)nRT ) (see Chapter 14), this energy does not change. Thus:
in other words:
So what happens if the cylinder shown in Fig. 15.5, immerse in a hot bath? Thermal energy ( Q ) must pass into the apparatus, and since the temperature of the gas remains constant, all this thermal energy must be converted into work done by the system. Let's say, for example, you have a mole of helium at a temperature of 20°C, and, just for fun, you decide to increase its volume from ( V_0 ) = 0.010 m3 to ( V_1 ) = 0.020 m3. How much work will the gas do when it expands? All you need to do is plug in the numbers into the formula:
The work done by the gas is 1690 J. The change in its internal energy is 0 J, as always in an isothermal process. And since ( Q=W ), the thermal energy added to the gas is also equal to 1690 J
In an adiabatic process, the total thermal energy of the system remains constant. Look at fig. 15.7, which shows a cylinder surrounded by insulating material. Thermal energy does not leave the system, so if a change occurs, it is adiabatic.
When calculating the work done in an adiabatic process, you can say that ( Q ) = 0, thus:
Since the internal energy ( U ) of an ideal gas is equal to ( (3/2)nRT ) (see Chapter 14), then the work done is:
where ( T_0 ) and ( T_1 ) mean the initial and final temperatures, respectively. Thus, if a gas does work, it does so due to a change in temperature—as the temperature drops, the gas does work on the surrounding bodies. In Fig. Figure 15.8 shows a graph of pressure versus volume during an adiabatic process. The adiabatic curve shown in this figure, called an adiabatic curve, is different from isothermal curves, called isotherms. The work done when the total thermal energy of the system is constant is the region under the adiabatic (see Fig. 15.8).
The initial values of pressure and volume can be related to their final values using the following formula:
What is ( gamma )? This is the ratio ( C_p/C_v ) of two specific heat capacities of an ideal gas: in the numerator - the heat capacity at constant pressure ( C_p ), and in the denominator - the heat capacity at constant volume (C_v). Specific heat capacity is the ratio of the thermal energy received by a body of unit mass to the corresponding increment in its temperature; You can learn more about this in Chapter 13. To calculate specific heat capacity, you need to find the amount of thermal energy ( Q ) required to change the temperature of a body of unit mass by ( Delta T ), i.e. ( c=Q/mDelta T ), where ( c ), ( m ) and ( Delta T ) mean specific heat capacity, mass and temperature change, respectively. However, now it is more convenient to use molar specific heat capacity, which is defined as specific heat, but is calculated not per unit mass, but per mole. It is designated by the symbol ( C ) and is measured in J/(mol K). So, the molar specific heat is used together with the number of moles ( n ) rather than the mass ( m ):
How to find ( C )? We need to calculate two different quantities: ( C_mathrm{p} ) (at constant pressure) and ( C_mathrm{v} ) (at constant volume). According to the first law of thermodynamics (see the previous section of this chapter), ( Q=Delta U+W ). Therefore, it is enough to just express ( Delta U ) through ( T ). The work performed ( W ) is equal to ( PDelta!V ), then at constant volume ( W ) = 0. And the change in internal energy of an ideal gas is ( (3/2)nRDelta T ) (see chapter 14), therefore ( Q ) at constant volume is expressed by the following formula:
At constant pressure, work ( W ) is equal to (PDelta!V). And since ( PV= nRT ), then ( W=P(V_1-V_0)=nR(T_1-T_0) ). Therefore, ( Q ) at constant pressure is expressed by the following formula:
How can we obtain from all this the values of the molar specific heats? As we already know, ( Q=CnDelta T ), therefore ( C=Q/nDelta T ). Dividing the previous two formulas by ( nDelta T ), we get:
You now have the molar specific heats of an ideal gas. The ratio you need ( gamma ) is equal to the ratio of these two formulas:
You can relate pressure and volume at any two points of the adiabatic process (see the previous section on the adiabatic process) in this way:
For example, if at first 1 liter of gas was under a pressure of 1 atm, and after an adiabatic change (when there is no exchange of thermal energy), the volume of the gas became 2 liters, then what should the new pressure ( P_1 ) be? By a simple algebraic operation of division by ( V_1^{5/3} ) we leave only ( P_1 ) on the left side of the equality and get:
Substituting numerical values into this formula, we get:
So, the new pressure should be 0.314 atmospheres.
Gcal and Gcal/h: what is the difference
If it is necessary to calculate the consumer's payment for state heat and power services (house heating, hot water), the value Gcal/h is used. It denotes a reference to time - how many Gigacalories are consumed during heating for a given period of time. Sometimes it is also replaced by Gcal/m3 (how much energy is needed to transfer heat to a cubic meter of water).
The value of Gcal/h can be calculated independently using this formula:
Q=V*(T1 – T2)/1000, where
- Q – amount of thermal energy;
- V – volume of liquid consumption in cubic meters/tons;
- T1 is the temperature of the incoming hot liquid, which is measured in degrees Celsius;
- T2 – temperature of the incoming cold liquid, similar to the previous indicator;
- 1000 is an auxiliary coefficient that simplifies calculations by eliminating numbers in the tenth digit (automatically converts kcal to Gcal).
This formula is often used to construct the operating principle of heat meters in private apartments, houses or enterprises. This measure is necessary when the cost of this utility service sharply increases, especially when calculations are generalized based on the area/volume of the room that is heated.
If a closed type system is installed in the room (hot liquid is poured into it once without additional water), the formula is modified:
Q= (( V1* (T1 – T2)) – (V2* (T2 – T)))/ 1000, where
- Q – amount of thermal energy;
- V1 – volume of consumed thermal substance (water/gas) in the pipeline through which it enters the system;
- V2 is the volume of thermal substance in the pipeline through which it returns;
- T1 – temperature in degrees Celsius in the inlet pipeline;
- T2 – temperature in degrees Aim in the outlet pipeline;
- T – cold water temperature;
- 1000 – auxiliary coefficient.
This formula is based on the difference between the inlet and outlet values of the coolant in the room.
Depending on the use of a particular energy source, as well as the type of thermal substance (water, gas), alternative calculation formulas are also used:
- Q= (( V1* (T1 – T2)) + (V1 – V2)*( T2 – T))/1000
- Q= (( V2* (T1 – T2)) + (V1 – V2)*(T1 – T))/1000
In addition, the formula changes if electrical devices are included in the system (for example, heated floors).
Definition [edit | edit code]
The amount of heat is included in the mathematical formulation of the first law of thermodynamics, which can be written as Q = A + ΔU. Here Δ U is the change in the internal energy of the system, Q is the amount of heat transferred to the system, and A is the work done by the system. However, the definition of heat must indicate the method of its measurement, regardless of the first principle. Since heat is the energy transferred during heat exchange, a test calorimetric body is needed to measure the amount of heat. By changing the internal energy of the test body, it will be possible to judge the amount of heat transferred from the system to the test body. Without the use of a test body, the first principle loses the meaning of a meaningful law and turns into a determination of the amount of heat that is useless for calculations.
Let in a system consisting of two bodies X and Y, body Y (test) is enclosed in a rigid adiabatic shell. Then it is not capable of performing macroscopic work, but can exchange energy (that is, heat) with body X. Let us assume that body X is also almost completely enclosed in an adiabatic, but not rigid shell, so that it can perform mechanical work, but can only exchange heat with Y. The amount of heat
, transferred to body X in a certain process, is the quantity QX = − Δ UY =-Delta U_>, where Δ UY > is the change in the internal energy of body Y. According to the law of conservation of energy, the total work done by the system is equal to the decrease in the total internal energy of the system of two bodies: A = − Δ U x − Δ U y -Delta U_>, where A is the macroscopic work done by body X, which allows us to write this relation in the form of the first law of thermodynamics: Q = A + Δ U x > .
| Types of energy: | ||
| Mechanical | Potential Kinetic | |
| ‹ ♦ › | Internal | |
| Electromagnetic | Electrical Magnetic | |
| Chemical | ||
| Nuclear | ||
| G | Gravitational | |
| ∅ | Vacuum | |
| Hypothetical: | ||
| Dark | ||
| See also: Law of Conservation of Energy | ||
Thus, the amount of heat introduced in phenomenological thermodynamics can be measured by means of a calorimetric body (the change in internal energy of which can be judged by the reading of the corresponding macroscopic device). From the first law of thermodynamics it follows that the introduced definition of the amount of heat is correct, that is, the independence of the corresponding quantity from the choice of test body Y and the method of heat exchange between bodies. With this determination of the amount of heat, the first law becomes a meaningful law that allows experimental verification, since all three quantities included in the expression for the first law can be measured independently [3].
How are Gcal calculated for hot water and heating?
Heating is calculated using formulas similar to the formulas for finding the value of Gcal/h.
An approximate formula for calculating payment for warm water in residential premises:
P i gv = Vi gv * T x gv + (V v cr * Vi gv / ∑ Vi gv * T v cr)
Values used:
- P i gv – the required value;
- V i gv – volume of hot water consumption for a certain time period;
- T x gw – established tariff fee for hot water supply;
- V v gv – the volume of energy expended by the company that heats it and supplies it to residential/non-residential premises;
- ∑ V i gw – the sum of warm water consumption in all rooms of the house in which the calculation is made;
- T v gv – tariff payment for thermal energy.
This formula does not take into account the atmospheric pressure indicator, since it does not significantly affect the final desired value.
The formula is approximate and is not suitable for independent calculation without prior consultation. Before using it, you need to contact local utility services for clarification and adjustment - perhaps they use other parameters and formulas for calculation.
We strive for thermal equilibrium: the zero law of thermodynamics
The basic laws of thermodynamics start from zero. This numbering may seem strange, since few things in everyday life begin this way (“Be careful on the zero step...”), but, you know, physicists like their traditions. So, the zero law of thermodynamics states that two bodies are in thermal equilibrium if they can transfer heat to each other, but do not. (In Russian-language scientific literature, the zeroth law of thermodynamics is also called the general law of thermodynamics. — Ed.)
For example, if you and the water in the swimming pool you are in are at the same temperature, then no heat is transferred from you to the water or from the water to you (although such transfer is possible). Your body and the pool are in thermal equilibrium. However, if you jump into a pool in winter, breaking through its ice crust, then at first you are unlikely to be in thermal equilibrium with its water. However, you don't want this. (Don't try this physical experiment at home!)
To detect thermal equilibrium (especially in frozen pools where you are about to jump), you need to use a thermometer. Use it to measure the temperature of the pool water, and then measure your temperature. If both temperatures coincide (in other words, there is thermal equilibrium: yours with the thermometer, and the thermometer with the water in the pool), then you are in thermal equilibrium with the pool water.
The use of a thermometer shows: two bodies that are in thermal equilibrium with a third are also in thermal equilibrium with each other; Here is another formulation of the zero beginning.
Among other things, the zero principle contains the idea that temperature is an indicator of thermal equilibrium. The fact that the two bodies mentioned in the zeroth law are in thermal equilibrium with the third gives everything needed by giving the assignment of a temperature scale, for example the Kelvin scale. Well, from a physical point of view, the zeroth law sets a reference point, stating that there is generally no heat flow between two bodies that have the same temperature.
Metering devices for houses and apartments
A special device allows you to accurately calculate tariffs for water supply, electricity, gas and heat. Users are allowed to install a heat meter to record heat energy consumption. The device measures in Gcal/h, kW/h and kJ/h. Popular today.
Vane meters
The vane meter operates effectively at temperatures below 22 degrees.
The meter has the form of a mechanism with a perpendicular axis of rotation. The model is characterized by low sensitivity, which allows you to accurately measure heat costs. The regulators are suitable for rooms with good thermal insulation and temperatures of +26 degrees. The vane device, when adjusting the temperature up to +22 degrees, counts a minimum of Gcal.
Advantages:
- inexpensive cost;
- power supply from batteries;
- ease of use;
- accuracy of measurements.
Minuses:
- risk of breakdowns due to water hammer;
- rapid wear of the mechanism;
- increased pressure in the system;
- When the impeller jams, the water flow is not allowed to pass through.
Vane-type devices are suitable for taking readings when a small volume of water is used.
Devices with jump recorders
Electronic devices are more expensive, but they count gigacalories more accurately.
The pulse device takes readings remotely from 2-16 channels, so it is suitable for a private or apartment building. Data recording and transmission is carried out on an LCD monitor, via a plug-in interface, to a laptop or computer using a network cable, or via a GSM network.
The scenario for which readings need to be measured is specified by the user. Ultrasonic devices can be connected to the water and gas supply system, are part of the ASKUE system, or can be combined with the “smart home” system.
Advantages:
- many options for public and private measurements;
- possibility of integration into several accounting systems;
- strength due to the absence of moving parts;
- beautiful appearance and compactness;
- protection from dust and moisture – the meter can be placed in the kitchen or outdoors;
- durable body;
- self-diagnosis functions for problems;
- extensive communication;
- execution with or without a removable computing unit;
- the period between inspections is 6 years, between replacements is 10 years.
Minuses:
- high price;
- communication capabilities depend on the specifics of the output;
- costs for the purchase of flow meters, pressure sensors, remote control modules for basic equipment.
For outdoor use, models with difference recorders with a moisture protection level of IP 68 are suitable.
What is all this for?
The problem should be considered from two points of view - from the point of view of apartment buildings and private ones. Let's start with the first ones.
Apartment buildings
There is nothing complicated here: gigacalories are used in thermal calculations. And if you know how much thermal energy remains in the house, then you can present the consumer with a specific bill. Let's give a small comparison: if centralized heating operates in the absence of a meter, then you have to pay according to the area of the heated room. If there is a heat meter, this in itself implies a horizontal wiring type (either collector or serial): two risers are brought into the apartment (for “return” and supply), and the intra-apartment system (more precisely, its configuration) is determined by the residents. This kind of scheme is used in new buildings, thanks to which people regulate the consumption of thermal energy, making a choice between savings and comfort.
Let's find out how this adjustment is carried out.
1. Installation of a general thermostat on the return line. In this case, the flow rate of the working fluid is determined by the temperature inside the apartment: if it decreases, the flow rate will accordingly increase, and if it increases, it will decrease.
2. Throttling of heating radiators. Thanks to the throttle, the passage of the heating device is limited, the temperature decreases, and therefore the consumption of thermal energy is reduced.
Private houses
We continue to talk about calculating Gcal for heating. Owners of country houses are interested, first of all, in the cost of a gigacalorie of thermal energy obtained from one or another type of fuel. The table below may help with this.
Table. Comparison of cost of 1 Gcal (including transport costs)
* - prices are approximate, since tariffs may differ depending on the region, moreover, they are constantly growing.
How to calculate Gcal for heating - the correct calculation formula
Often, one of the problems that consumers face both in private buildings and in apartment buildings is that the consumption of thermal energy obtained in the process of heating a home is very large. In order to save yourself from the need to overpay for excess heat and to save money, you should determine exactly how the amount of heat for heating should be calculated. Conventional calculations will help solve this, with the help of which it will become clear what volume the heat entering the radiators should have. This is exactly what will be discussed further.
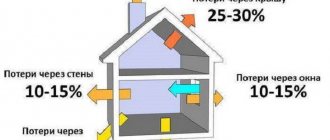
How do people use the thermal energy of the Earth's interior?
Therefore, heat in the bowels of the earth is retained even in winter, and this heat can be used to heat buildings. To do this, you will need to make a well and purchase a special heat pump. A heat pump installed in a house converts the energy of soil, water, and air into heat, which heats the house.
Sources:
- https://ru.uzvisit.com/1444-thermal-energy
- https://10i5.ru/raznoe/chto-takoe-teplovaya-energiya.html
- https://novoe-info.ru/chto-takoe-teplovaya-energiya/
- https://MadEnergy.ru/stati/teplovaya-energiya-edinicy-izmereniya-i-ix-pravilnoe-ispolzovanie.html
- https://fizi4ka.ru/fizika-s-formulami/glava-15-teplovaja-jenergija-i-rabota-nachala-termodinamiki.html
- https://RosSchet.ru/articles/pochemu_v_raschetakh_tepla_ispolzuyutsya_gkal_i_kvt/
General principles for performing Gcal calculations
Calculating kW for heating involves performing special calculations, the procedure of which is regulated by special regulations. Responsibility for them lies with utility organizations that are able to help with this work and give an answer regarding how to calculate Gcal for heating and the decoding of Gcal.
Of course, such a problem will be completely eliminated if there is a hot water meter in the living room, since it is in this device that there are already pre-set readings that display the heat received. By multiplying these results by the established tariff, it is possible to obtain the final parameter of the heat consumed.
Option 2
Now we will calculate payments in conditions where the house is equipped with a common heating meter, and some of the apartments are also equipped with individual meters. As in the previous case, the calculation will be carried out according to two positions (thermal energy consumption for housing and ODN).
We will need formula No. 1 and No. 2 (accrual rules according to controller readings or taking into account heat consumption standards for residential premises in Gcal). Calculations will be carried out relative to the area of the residential building and apartment from the previous version.
Calculation 1
Formula No. 1: 1.3 x 1,400 = 1,820 rubles, where:
- 1.3 gigacalories – individual meter readings;
- RUR 1,1820 – approved tariff.
https://youtube.com/watch?v=dFLW96z0YVk
Formula No. 2: 0.025 x 70 x 1,400 = 2,450 rubles, where:
- 0.025 Gcal – standard indicator of heat consumption per 1 m² of area in an apartment;
- 70 m² – square footage of the apartment;
- 1,400 rub. – tariff for thermal energy.
Next, we calculate the second component of our payment (ODN) using two formulas - No. 13 (volume of service) and No. 10 (heating cost).
Calculation 2
Formula No. 13: (300 – 12 – 7,000 x 0.025 – 9 – 30) x 75 / 8,000 = 1.425 gcal, where:
- 300 gcal – readings of the common house meter;
- 12 Gcal – the amount of thermal energy used to heat non-residential premises;
- 6,000 m² – the sum of the area of all residential premises;
- 0.025 – standard (heat energy consumption for apartments);
- 9 Gcal – the sum of indicators from the meters of all apartments that are equipped with metering devices;
- 35 Gcal – the amount of heat spent on supplying hot water in the absence of a centralized supply;
- 70 m² – apartment area;
- 8,000 m² – total area (all residential and non-residential premises in the house).
https://youtube.com/watch?v=tGvIg-I1QCU
Please note that this option includes only the actual volumes of energy consumed and if your house is equipped with a centralized hot water supply, then the amount of heat spent on hot water supply needs is not taken into account. The same applies to non-residential premises: if they are not in the house, then they will not be included in the calculation
Next comes the calculation of the payment for heating by multiplying the volume of heat by the tariff according to formula No. 10: 1.425 x 1,400 = 1,995 rubles, where:
- 1.425 gcal – amount of heat (AT);
- 1,400 rub. – approved tariff.
As a result of the calculations, we found out that the full payment for heating will be:
- 1820 + 1995 = 3,815 rubles. - with an individual counter.
- 2,450 + 1995 = 4,445 rubles. - without an individual device.
Calculation procedure when calculating heat consumption
In the absence of such a device as a hot water meter, the formula for calculating heat for heating should be as follows: Q = V * (T1 - T2) / 1000. The variables in this case display values such as:
- Q in this case is the total amount of heat energy;
- V is the indicator of hot water consumption, which is measured either in tons or in cubic meters;
- T1 – temperature parameter of hot water (measured in standard degrees Celsius). In this case, it would be more appropriate to take into account the temperature that is characteristic of a certain operating pressure. This indicator has a special name - enthalpy. But in the absence of the required sensor, you can take as a basis the temperature that will be as close as possible to the enthalpy. As a rule, its average varies between 60 and 65°C;
- T2 in this formula is the temperature indicator of cold water, which is also measured in degrees Celsius. Due to the fact that getting to the pipeline with cold water is very problematic, such values are determined by constant values, which differ depending on the weather conditions outside the home. For example, in the winter season, that is, at the height of the heating season, this value is 5°C, and in the summer, when the heating circuit is turned off, it is 15°C;
- 1000 is a common coefficient that can be used to get the result in gigacalories, which is more accurate, rather than in regular calories.
Calculation of Gcal for heating in a closed system, which is more convenient for operation, should be done in a slightly different way. The formula for calculating heating of a room with a closed system is as follows: Q = ((V1 * (T1 - T)) - (V2 * (T2 - T))) / 1000.
- Q – still the same volume of thermal energy;
- V1 is the coolant flow parameter in the supply pipe (the heat source can be either ordinary water or steam);
- V2 – volume of water flow in the outlet pipeline;
- T1 – temperature value in the coolant supply pipe;
- T2 – outlet temperature indicator;
- T – temperature parameter of cold water.
Heat capacity
The heat capacity c of a given substance means the number of calories required to heat 1 kg of a substance by 1 ° C. To heat g kg of a substance having a heat capacity c by t degrees, g is required. With. t calories
Heat capacity of various substances at 15°C
| Alcohol | 0,58 | Aluminum | 0,214 | Benzene | 0,41 |
| Bronze | 0,09 | Water | 0,999 | water vapor | 0,48 |
| Gypsum | 0,20 | Granite | 0,20 | Graphite | 0,2 |
| Charcoal | 0,2 | Iron | 0,111 | Gold | 0,031 |
| Kerosene | 0,51 | Brass | 0,090 | Ice | 0,463 |
| Coal | 0,31 | Machine oil | 0,40 | Copper | 0,092 |
| Marble | 0,20 | Nikkel | 0,105 | Tin | 0,054 |
| Platinum | 0,032 | Mercury | 0,0333 | Lead | 0,031 |
| Sulfur | 0,17 | Sulfuric acid | 0,33 | Silver | 0,055 |
| Turpentine | 0,42 | Steel | 0,114 | Glass | 0,19 |
| Antimony | 0,050 | Zinc | 0,002 | Ether | 0,56 |
Heat capacity is not constant: with increasing temperature it increases slightly for all bodies except mercury, for which it decreases
Other methods for calculating heat volume
You can calculate the amount of heat entering the heating system in other ways.
The formula for calculating heating in this case may differ slightly from the above and have two options:
- Q = ((V1 * (T1 - T2)) + (V1 - V2) * (T2 - T)) / 1000.
- Q = ((V2 * (T1 - T2)) + (V1 - V2) * (T1 - T)) / 1000.
All variable values in these formulas are the same as before.
Based on this, we can say with confidence that the calculation of kilowatts of heating can be done on your own. However, do not forget about consultation with special organizations responsible for supplying heat to homes, since their principles and calculation system may be completely different and consist of a completely different set of measures.
Having decided to construct a so-called “warm floor” system in a private house, you need to be prepared for the fact that the procedure for calculating the volume of heat will be much more complicated, since in this case it is necessary to take into account not only the features of the heating circuit, but also provide for the parameters of the electrical network from which and the floor will be heated. At the same time, the organizations responsible for monitoring such installation work will be completely different.
Many owners often face the problem of converting the required amount of kilocalories into kilowatts, which is due to the use of measuring units in the international system called “C” by many auxiliary aids. Here you need to remember that the coefficient converting kilocalories into kilowatts will be 850, that is, in simpler terms, 1 kW is 850 kcal. This calculation procedure is much simpler, since calculating the required volume of gigacalories is not difficult - the prefix “giga” means “million”, therefore, 1 gigacalorie is 1 million calories.
In order to avoid errors in calculations, it is important to remember that absolutely all modern heat meters have some error, but often within acceptable limits. The calculation of such an error can also be done independently, using the following formula: R = (V1 - V2) / (V1 + V2) * 100, where R is the error of the common house heating meter. V1 and V2 are the parameters of water flow in the system already mentioned above, and 100 is the coefficient responsible for converting the resulting value into a percentage. In accordance with operational standards, the maximum permissible error may be 2%, but usually this figure in modern instruments does not exceed 1%.
Video description
About the intricacies of calculating heating fees in the following video:
Counter with difference recorder
The operation of the device is based on Bernoulli's law, which relates the speed of fluid flow and its pressure. In the meter, the path of water is blocked by a special retaining washer - a steel disk with a drilled hole of a known diameter.
When the water flow rate changes, the drop on the washer also changes, and the change occurs according to a quadratic law: if the flow rate doubles, then the drop on the washer increases 4 times. If the flow rate, for example, is reduced by 3 times, then the throttled pressure on the washer is reduced by 9 (3²) times.
The registration meter is equipped with an electronic unit that allows you to determine the temperature and flow rate of the coolant, as well as the actual heat consumption. The device can be connected to a computer and configured manually.
Types of electromagnetic heat meters Source energo-climat.com
Physical meaning of the heating consumption standard
Apartment buildings in the legislation of the Russian Federation, including for the purpose of calculating the volume of heat energy consumption for heating, are considered as indivisible units. That is, an apartment building is a single thermal engineering facility that consumes heat energy to heat the premises included in it. And it is the total volume of heat energy consumed by the entire house that is important when calculating the utility service provider (ICU) with the resource supply organization (RSO).
The rules for establishing and determining standards for the consumption of utility services, approved by the RF PP dated May 23, 2006 N306 (hereinafter referred to as Rules 306), in order to calculate the standard consumption of utility services for heating, first provide for the calculation of the amount of thermal energy required for heating an apartment building or residential building during the year (clause 19 of Appendix 1 to Rule 306, formula 19). The year was chosen as the period for which the calculation is made in order to further obtain the average value of the standard heat energy consumption per month, since in different calendar months the heat energy consumption for heating will, of course, be different, and payment according to the standard implies the same amount of payment for heating either within heating period, or evenly throughout the calendar year, depending on the method of payment for heating .
Since an apartment building consists of a set of residential and non-residential premises and common areas (common property), while the common property on the right of common ownership belongs to the owners of individual premises of the house, the entire volume of thermal energy entering the house is consumed by the owners of the premises of such a house. Consequently, payment for heat energy consumed for heating must be made by the owners of the apartment building premises. And here the question arises - how to distribute the cost of the entire volume of heat energy consumed by an apartment building among the owners of the premises of this apartment building?
Guided by the completely logical conclusions that the consumption of heat energy in each specific room depends on the size of such a room, the Government of the Russian Federation has established a procedure for distributing the volume of heat energy consumed by the entire house among the premises of such a house in proportion to the area of these premises. This procedure is provided for both by Rule 354 (distribution of readings from a common house heating meter in proportion to the shares of the premises of specific owners in the total area of all premises of the house owned) and Rule 306 when establishing heating consumption standards.
Paragraph 18 of Appendix 1 to Rule 306 states: “18. The consumption standard for heating utilities in residential and non-residential premises (Gcal per 1 sq.m. of the total area of all residential and non-residential premises in an apartment building or residential building per month) is determined by the following formula (formula 18):
,
where: - the amount of thermal energy consumed during one heating period by apartment buildings not equipped with collective (common building) heat energy metering devices, or residential buildings not equipped with individual thermal energy metering devices (Gcal), determined by formula 19; - the total area of all residential and non-residential premises in apartment buildings or the total area of residential buildings (sq.m); - a period equal to the duration of the heating period (the number of calendar months, including incomplete ones, in the heating period).”
Shrinkage
As metals solidify and cool, their dimensions change. The resulting tensions, caused by uneven cooling and unequal distribution of material, increase or decrease the dimensions on one side or the other of the casting
| Metal | Linear relative | Linear cm per 1m | Surface relative | Surface cm3 per 1m3 | Volume relative | Volume cm3 per 1m3 |
| Aluminum | 1:56 | 1,79 | 1:28 | 357 | 1:19 | 53590 |
| Aluminum bronze | 1:53 | 1,89 | 1:27 | 377 | 1:18 | 56610 |
| Bronze | 1:63 | 1,59 | 1:32 | 317 | 1:21 | 47610 |
| Bell met. | 1:65 | 1,54 | 1:33 | 308 | 1:22 | 46140 |
| Brass | 1:65 | 1,54 | 1:32 | 313 | 1:22 | 46140 |
| Copper | 1:125 | 0,80 | 1:63 | 160 | 1:42 | 24000 |
| Tin | 1:128 | 0,78 | 1:64 | 156 | 1:43 | 23400 |
| Steel | 1:50 | 2,00 | 1:25 | 400 | 1:17 | 60000 |
| Lead | 1:92 | 1,09 | 1:46 | 217 | 1:31 | 32610 |
| Zinc | 1:62 | 1,61 | 1:32 | 313 | 1:21 | 48300 |
| Cast iron | 1:96 | 1,04 | 1:48 | 208 | 1:32 | 31260 |
GHS and non-systemic units
| gigacalorie per hour to gigacalorie per second |
| gigacalorie per hour to kilocalorie per second |
| gigacalorie per hour to calories per second |
| gigacalories per hour to gigacalories per minute |
| gigacalorie per hour to kilocalorie per minute |
| gigacalories per hour to calories per minute |
| gigacalorie per hour to gigacalorie per hour |
| gigacalorie per hour to kilocalorie per hour |
| gigacalorie per hour to calories per hour |
| gigacalorie per hour to boiler horsepower (hp(S)) |
| gigacalorie per hour to electrical horsepower (hp(E)) |
| gigacalorie per hour to hydraulic horsepower |
| gigacalorie per hour to mechanical horsepower (hp(I)) |
| gigacalorie per hour to metric horsepower (hp(M)) |
| gigacalorie per hour to kilogram-force meter per second (kgf*m/s) |
| gigacalorie per hour to joule per second |
| gigacalorie per hour to joule per minute |
| gigacalorie per hour to joule per hour |
| gigacalorie per hour to erg per second |
| gigacalorie per hour to metric refrigeration ton (RT) |
| gigacalorie per hour to frigoria per hour (fg/h) |
Units: gigacalories per second / kilocalories per second / calories per second / gigacalories per minute / kilocalories per minute / calories per minute / gigacalories per hour / kilocalories per hour / calories per hour / boiler horsepower (hp(S)) / electric horsepower power (hp(E)) / hydraulic horsepower / mechanical horsepower (hp(I)) / metric horsepower (hp(M)) / kilogram-force meter per second (kgf*m/s) / joule per second / joule per minute / joule per hour / erg per second / metric refrigeration ton (RT) / frigoria per hour (fg/h) » open »» collapse »
Gigacalorie
As units of the amount of heat in technology, the joule (J), international calorie (cal) and multiple units are accepted: kilocalorie (kcal), megacalorie (Mcal), gigacalorie (Gcal): 1 cal 4 1868 J (exactly) 4 19 J; 1 kcal 1000 cal 4 19 kJ; 1 Mcal 1000 kcal 1,000,000 cal 4 19 MJ; 1 Gcal 1000 Mcal 1,000,000 kcal 1,000,000,000 cal 4 19 GJ.
The most important indicator characterizing a boiler room in the heat supply system to consumers is its thermal power (performance) - the total maximum power for all types of coolants supplied by the boiler room to consumers, expressed in gigacalories per hour.
Specific strength, unit - kilogram-force-centimeter per gram square meter per kilogram-force square centimeter per kilogram-force kilogram-force-second per square meter kilogram per second-meter kilogram-force per meter kilogram-force-meter per square centimeter kilogram-force centimeter per square centimeter Darcy kilogram per hour per meter-millimeter of water kilogram per hour per meter-0 1 atmosphere gram per hour per meter-millimeter of mercury cubic meter per hour per meter - millimeter of water teracalorie gigacalorie megacalorie kilocalorie calorie calorie thermochemical calorie per gram kilocalorie per kilogram calorie per gram degree Celsius kilocalorie per kilogram degree Celsius calorie per gram kelvin kilocalorie per kilogram kelvin kilogram-force meter per kilogram degree Celsius calorie per second kilocalorie per hour megacalorie per hour kilocalorie per hour per square meter megacalorie per hour per square meter kilocalorie per hour per cubic meter megacalorie per hour per cubic meter kilocalorie per hour per square meter-degree Celsius calorie per second per square centimeter-degree Celsius kilocalorie per hour per meter-degree Celsius calorie per second per centimeter degree Celsius ohm-square millimeter per meter curie curie per kilogram curie per gram curie per cubic meter curie per liter curie per milliliter curie per square meter curie per square centimeter rad kgf cm/g M2/KGS CM2/KGS kgf s / m2 kg / ( s-m) kgf / m kgf m / cm2 kgf cm / cm2 d KG / ( H - M - MM WOD.
In cases where great precision is not required, values are given in rounded figures. The same applies to the gigacalorie, since peak water boilers are labeled in this unit in terms of heating output.
The amount of heat is expressed in gigajoules or gigacalories. The latter unit continues to be widely used due to the ease of transition to this unit from the unit of mass and temperature.
Thus, the cost of heat transport consists of a number of cost items associated with the operation of heat pipelines and pumping substations; it fluctuates depending on local conditions. For example, in the Moscow Heating Network the cost of transporting one gigacalorie is 18 kopecks.
British and American units
| gigacalorie per hour to American refrigeration ton (USRT) |
| gigacalorie per hour to British thermal unit per second (BTU/s) |
| gigacalorie per hour to British Thermal Unit per minute (BTU/min) |
| gigacalorie per hour to British Thermal Unit per hour (BTU/hr) |
| gigacalorie per hour to foot pound-force per second (ft*lbf/s) |
Units: US refrigeration ton (USRT) / British thermal unit per second (BTU/s) / British thermal unit per minute (BTU/min) / British thermal unit per hour (BTU/hr) / foot pound-force per second (ft *lbf/s) » open »» collapse »
Features of self-calculation
Not all users know what “DHW heat energy” is in the receipt, and many do not trust the billing center and independently calculate the amount of heat energy consumed. In order to calculate everything at home and eliminate fraud, you must first find out: the fuel component in the receipt - what it is, how it is calculated.
To make the correct calculation, you need to know the current heating tariff. The absence or presence of a meter installed in the apartment also affects the result. If there are no meters, the standard indicator is taken as a basis.
If an apartment building has meters, then the total amount is calculated by multiplying the tariff by the meter readings. Everyone can quickly figure out “hot water supply: carrier” and “energy” - what they are, and how to correctly calculate the indicators.
You can submit data from meters onlinePHOTO: fednews.ruThe tariff for fuel is indicated in the receiptPHOTO: zvu-74.ru